Homework2

题目1

前四列是天气情况（阴晴 outlook，气温 temperature，湿度 humidity，风 windy）；最后一列是类标签，表示根据天气情况是否出去玩。

outlook	temperature	humidity	windy	play
sunny	hot	high	FALSE	no
sunny	hot	high	TRUE	no
rainy	cool	normal	TRUE	no
sunny	mild	high	FALSE	yes
sunny	cool	normal	FALSE	yes
rainy	mild	normal	FALSE	yes
overcast	cool	normal	TRUE	yes
rainy	cool	normal	FALSE	yes
rainy	mild	high	FALSE	yes
overcast	hot	high	FALSE	yes

outlook: sunny, rainy, overcast
temperature: hot mild cool
humidity: high, normal
windy TRUE, FALSE
play no, yes

(1) “信息熵”是度量样本集合纯度最常用的一种指标，假定当前样本集合 D 中第 k 类样本所占的比例为 𝑝_k（k=1, 2, …, K）,请问当什么条件下，D 的信息熵 Ent(D)取得最大，最大值为多少？
(2) 根据表中训练数据，基于信息增益决策树应该选哪个属性作为第一个分类属性？
(3) 对于含有连续型属性的样本数据，决策树和朴素贝叶斯分类能有哪些处理方法？
(4) 在分类算法的评价指标中，recall 和 precision 分别是什么含义？
(5) 若一批数据中有 3 个属性特征，2 个类标记，则最多可能有多少种不同的决策树？（不同决策树指同一个样本在两个两个决策下可能得到不同的类标记）

Answers:

1) 当p_k等概率时最大，为log_2K
2) 显然，K=2，p_{no}=0.3,p_{yes}=0.7因此，根节点的信息熵 Ent(D)=-0.3*log_2{0.3}-0.7*log_2{0.7}=0.88129 根据公式，分别计算Gain(D,outlook) = 0.157, Gain(D,temperature) = 0.281, Gain(D,humidity) = 0.035, Gain(D,windy) = 0.192 因此，应选temperature作为第一个分类属性。
3) 由于决策树和朴素贝叶斯分类都是对离散特征进行分类判别的方法，所以对连续型属性，他们都需要对其进行离散化处理。处理方法有二分法等离散化方式或根据数据集估计该特征的概率密度函数等。
4) recall是查全率，又称召回率，定义为TP/(TP+FN)，precision是查准率，又称准确率，定义为TP/(TP+FP)，式中TP是真阳性结果，FP是假阳性结果，FN是假阴性结果，因此，recall代表查到的正确结果占所有正确结果的比例，precision代表查到的所有结果中正确结果的比例。
5) 最多可能有6种。

import numpy as np
import pandas as pd

data1 = pd.DataFrame({  
    "outlook":['sunny','sunny','rainy','sunny','sunny','rainy','overcast','rainy','rainy','overcast'],
    "temperature":['hot','hot','cool','mild','cool','mild','cool','cool','mild','hot'],
    "humidity":['high','high','normal','high','normal','normal','normal','normal','high','high'],
    "windy":['FALSE','TRUE','TRUE','FALSE','FALSE','FALSE','TRUE','FALSE','FALSE','FALSE'],
    "play":['no','no','no','yes','yes','yes','yes','yes','yes','yes']
})
def Ent(data):
    p = pd.value_counts(data)/len(data)
    return sum(-p*np.log2(p))

ent_d = Ent(data1['play'])
print(ent_d)

def Gain(data,D,a):
    Ent_ = data.groupby(a).apply(lambda x:Ent(x[D]))
    p_ = pd.value_counts(data[a])/len(data[a])
    gain = Ent(data[D])-sum(Ent_ * p_)
    return gain

gain_o = Gain(data1,'play','outlook')
gain_t = Gain(data1,'play','temperature')
gain_h = Gain(data1,'play','humidity')
gain_w = Gain(data1,'play','windy')

print(gain_o)
print(gain_t)
print(gain_h)
print(gain_w)
# ent_d_o = Ent([0.4,0.4,0.2])
# ent_d_t = Ent([0.3,0.3,0.4])
# ent_d_h = Ent([0.5,0.5])
# ent_d_w = Ent([0.3,0.7])

# def Gain(ent_d,ent_l,plist):
#     gain = ent_d
#     for ent in ent_l:
#         gain -= ent_l
#     return gain

Result

0.8812908992306927
0.15677964944703948
0.2812908992306927
0.034851554559677256
0.19163120400671674

题目2

已知正例点 x1 = (2，3)T，x2 = (3, 2)T，负例点 x3 = (1, 1)T

(1) 试用 SVM 对其进行分类，求最大间隔分离超平面，并指出所有的支持向量。
(2) 现额外有一个点能被 SVM 正确分类且远离决策边界，如果将该点加入到训练集，SVM 的决策边界会受影响吗？为什么？

Answers

1) SVM：线性超平面方程w^T+b=0，记为(w,b) 要找到具有“最大间隔”的划分超平面，也就是要找到满足约束的参数w和b使\gamma最大，即\mathop{max}\limits_{(w,b)} \frac{2}{||w||} \\s.t. y_i(w^Tx_i+b)\geq1, i=1,2,...,m

可重写为\mathop{min}\limits_{(w,b)} \frac{1}{2}||w||^2 \\s.t. y_i(w^Tx_i+b)\geq1, i=1,2,...,m

x_1=(2,3)^T,y_1=1\\x_2=(3,2)^T,y_2=1\\x_3=(1,1)^T,y_3=-1

2*w1+3*w2+b\geq1\\3*w1+2*w2+b\geq1\\-1(w1+w2+b)\geq1

解得w1=w2=\frac{2}{3}，b=-\frac{7}{3}

x1 x2 x3均为支持向量

2) 不会，因为影响SVM超平面的向量仅有距离边界最近的一系列支持向量，如果该点能被正确分类且远离决策边界，则边界不会有变化。

题目3

下表是一个由 15 个贷款申请训练数据，数据包括贷款申请人的四个特征属性：分别是年龄，是否有工作，是否有自己的房子以及信贷情况，表的最后一列为类别，是否同意贷款。

1）请根据上表的训练数据，以错误率作为划分标准来构建预测是否进行放贷的决策树。
2）按照所构建的决策树，对属性值为（中年，无工作，无自己的房子，信贷情况好）的申请者是否进行放贷
3）在构建决策树的时候，可能会出现过拟合的问题，有哪些方法可以避免或者解决？
4）对于含有连续型属性的样本数据，决策树有哪些处理方法？

Answers

1) 以错误率为划分标准，分别对四个属性进行划分计算错误率：

年龄：青年|中年老年 5/15
有工作：否|是 4/15
有房子：否|是 3/15
信贷情况：一般|好非常好 3/15
因此，节点1应使用是否有自己的房子

节点1 左侧分支：
年龄：青年|中年老年 /9
有工作：否|是 0/9
信贷情况：一般|好非常好 3/9

节点1 右侧分支：全部划分为同意

因此，节点2应使用是否有工作
左侧分支全部拒绝，右侧分支全部同意

2) 不放贷。
3) 进行预剪枝，对划分前后的泛化性能进行估计，在训练中防止对节点的过度划分。或进行后剪枝，利用验证集对节点自底向上逐一考察，从而去除过拟合的分支。
4) 对连续数据进行离散化，如依照数值区间离散化到类别。或用连续值的范围进行划分，即二分法等操作。

题目4

请评价两个分类器 M1 和 M2 的性能。所选择的测试集包含 26 个二值属性，记作 A 到 Z。表中是模型应用到测试集时得到的后验概率（图中只显示正类的后验概率）。因为这是二类问题，所以 P(-)=1-P(+),P(-|A,…,Z)=1-P(+|A,…,Z)。假设需要从正类中检测实例
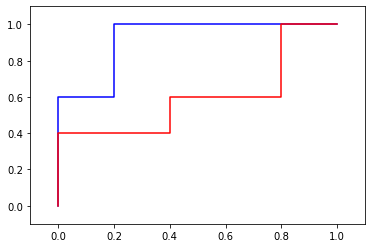
1) 画出 M1 和 M2 的 ROC 曲线（画在一幅图中）。哪个模型更多？给出理由。
2) 对模型 M1，假设截止阈值 t=0.5。换句话说，任何后验概率大于 t 的测试实例都被看作正例。计算模型在此阈值下的 precision，recall 和 F-score。
3) 对模型 M2 使用相同的截止阈值重复（2）的分析。比较两个模型的 F-score，哪个模型更好？所得结果与从 ROC 曲线中得到的结论一致吗？
4) 使用阈值 t=0.1 对模型 M2 重复（2）的分析。t=0.5 和 t=0.1 哪一个阈值更好？该结果和你从 ROC 曲线中得到的一致吗？

Answers

1) M1更多。可以看出相同阈值时M1表现更好，其ROC曲线下面积也超过M2
2) 模型M1在阈值t=0.5下的precision为0.75，recall为0.6，F-score为0.667
3) 模型M2在阈值t=0.5下的precision为0.5，recall为0.8，F-score为0.6154,模型M1更好，与ROC曲线一致
4) 模型M2在阈值t=0.1下的precision为0.5，recall为1.0，F-score为0.667,模型M1更好，与ROC曲线一致

#1
import numpy as np
import matplotlib.pyplot as plt

def prf(gt,p,th):
    tp = 0
    fp = 0
    tn = 0
    fn = 0
    for i in range(len(gt)):
        if(p[i]>th):#判为阳性
            if(gt[i] == 1):#真阳性
                tp += 1
            else:#假阳性
                fp += 1
        else:#判为阴性
            if(gt[i] == 1):#假阴性
                fn += 1
            else:
                tn += 1
    return [tp/()]

# 以1代表+，0代表-，输入p均为P(+)
def fpr(gt,p,th):# 假正率，FP/FP+TN，横坐标
    fp = 0
    tn = 0
    for i in range(len(gt)):
        if(p[i]>th):#判为阳性
            if(gt[i] == 1):#真阳性
                pass
                #tp += 1
            else:#假阳性
                fp += 1
        else:#判为阴性
            if(gt[i] == 1):#假阴性
                pass
                #fn += 1
            else:#真阴性
                tn += 1
    return fp/(fp+tn)

def tpr(gt,p,th):# 真正率，TP/TP+FN，纵坐标
    tp = 0
    fn = 0
    for i in range(len(gt)):
        if(p[i]>th):#判为阳性
            if(gt[i] == 1):#真阳性
                tp += 1
            else:#假阳性
                pass
                #fp += 1
        else:#判为阴性
            if(gt[i] == 1):#假阴性
                fn += 1
            else:#真阴性
                pass
                #tn += 1
    return tp/(tp+fn)

def corr(gt,p):
    N = 101
    cors = np.zeros((2,N))
    th = np.linspace(0,1,N)
    for i in range(N):
        cors[0][i]=fpr(gt,p,th[i])
        cors[1][i]=tpr(gt,p,th[i])
    return cors
gt = [1,1,0,0,1,1,0,0,1,0]
p_m1 = np.array([0.73,0.69,0.44,0.55,0.67,0.47,0.08,0.15,0.45,0.35])
p_m2_ = np.array([0.61,0.03,0.68,0.31,0.45,0.09,0.38,0.05,0.01,0.04])
p_m2 = 1-p_m2_
print(p_m2)
c1 = corr(gt,p_m1)
c2 = corr(gt,p_m2)
plt.plot(c1[0], c1[1],color='b')
plt.plot(c2[0], c2[1],color='r')
plt.xlim([-0.1, 1.1])
plt.ylim([-0.1, 1.1])
plt.show()
print("蓝色为M1-ROC，红色为M2-ROC")

Result

[0.39 0.97 0.32 0.69 0.55 0.91 0.62 0.95 0.99 0.96]

蓝色为M1-ROC，红色为M2-ROC

#2,3,4
import numpy as np
# 以1代表+，0代表-，输入p均为P(+)
def prf(gt,p,th):
    tp = 0
    fp = 0
    tn = 0
    fn = 0
    for i in range(len(gt)):
        if(p[i]>th):#判为阳性
            if(gt[i] == 1):#真阳性
                tp += 1
            else:#假阳性
                fp += 1
        else:#判为阴性
            if(gt[i] == 1):#假阴性
                fn += 1
            else:#真阴性
                tn += 1
    precision = tp/(tp+fp)
    recall = tp/(tp+fn)
    fscore = 2*precision*recall/(precision+recall)
    return precision,recall,fscore

gt = [1,1,0,0,1,1,0,0,1,0]
p_m1 = np.array([0.73,0.69,0.44,0.55,0.67,0.47,0.08,0.15,0.45,0.35])
p_m2_ = np.array([0.61,0.03,0.68,0.31,0.45,0.09,0.38,0.05,0.01,0.04])
p_m2 = 1-p_m2_
print("#2 P={0[0]},R={0[1]},F={0[2]}".format(prf(gt,p_m1,0.5)))
print("#3 P={0[0]},R={0[1]},F={0[2]}".format(prf(gt,p_m2,0.5)))
print("#4 P={0[0]},R={0[1]},F={0[2]}".format(prf(gt,p_m2,0.1)))

Result

#2 P=0.75,R=0.6,F=0.6666666666666665
#3 P=0.5,R=0.8,F=0.6153846153846154
#4 P=0.5,R=1.0,F=0.6666666666666666

题目5

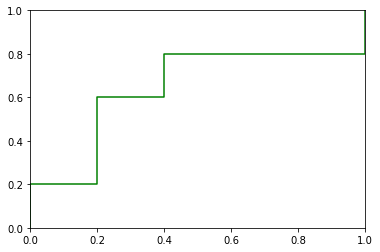
下图中数据元组已经按分类器返回概率值的递减顺序排序。对于每个元组，计算真正例（TP）、假正例（FP）、真负例（TN）和假负例（FN）的个数。计算真正例率（TPR）和假正例率（FPR）。为该数据绘制 ROC 曲线。

元组号	类	概率
1	P	0.95
2	N	0.85
3	P	0.78
4	P	0.66
5	N	0.60
6	P	0.55
7	N	0.53
8	N	0.52
9	N	0.51
10	P	0.40

gt_5 = [1,0,1,1,0,1,0,0,0,1]
p_5 = np.array([0.95,0.85,0.78,0.66,0.60,0.55,0.53,0.52,0.51,0.40])

c5 = corr(gt_5,p_5)
plt.plot(c5[0], c5[1],color='g')
plt.xlim([-0., 1.])
plt.ylim([-0., 1.])
plt.show()

Result

题目6

假设两个预测模型 M 和 N 之间进行选择。已经在每个模型上做了 10 轮 10-折交叉验证，其中在第 i 轮，M 和 N 都是用相同的数据划分。
M 得到的错误率为 30.5、32.2、20.7、20.6、31.0、41.0、27.7、28.0、21.5、28.0。
N 得到的错误率为 22.4、14.5、22.4、19.6、20.7、20.4、22.1、19.4、18.2、35.0。评述在 1%的显著水平上，一个模型是否显著地比另一个好。

Answers

对每对错误率求差，可得Δ=[8.1,17.7,-1.7,1.0,10.3,20.6,5.6,8.6,3.3,-7]
\mu=6.65
\sigma^2=63.6225
\tau=\lvert\frac{\sqrt{10}*\mu}{\sigma}\rvert \\=2.6364

10次10折在1%的显著水平上临界值为3.250，所以在1%的显著水平上，模型N没有显著比M好。

import numpy as np
import pandas as pd
delta = [8.1,17.7,-1.7,1.0,10.3,20.6,5.6,8.6,3.3,-7]
u = np.average(delta)
print("u=",u)
s = np.var(delta)
print("s=",s)
t = np.abs(np.sqrt(10)*u/np.sqrt(s))
print("t=",t)

Result

u= 6.65
s= 63.6225
t= 2.636430214066993

【USTCStudy】数据科学基础课程第二次作业

Homework2

题目1

Answers:

Result

题目2

Answers

题目3

Answers

题目4

Answers

Result

Result

题目5

Result

题目6

Answers

Result

typecho Database Query Error(转载备查，主要是记一下命令)

【USTCStudy】网络安全协议大作业：论文翻译——DNS Cache Poisoning Attack Reloaded: Revolutions with Side Channels

SakurakoujiLuna

Comments | NOTHING

Homework2

题目1

Answers:

Result

题目2

Answers

题目3

Answers

题目4

Answers

Result

Result

题目5

Result

题目6

Answers

Result

typecho Database Query Error(转载备查，主要是记一下命令)

【USTCStudy】网络安全协议大作业：论文翻译——DNS Cache Poisoning Attack Reloaded: Revolutions with Side Channels

SakurakoujiLuna

Comments | NOTHING

你想搜索什么...